Über typische Denkfallen, in die man hineintappen kann, wenn man nach kreativen Lösungen sucht.
Drei typische menschliche Denkfallen, in die man oft hineintappt, wenn man nach kreativen Lösungen für ein Problem sucht, hatten wir schon in der ersten Folge vorgestellt. Die Beispiele stammen aus Experimenten der psychologischen Problemlösungsforschung. Hier nun weitere:
Aufmerksamkeitsfokus
Soll man ein Problem lösen, konzentriert man sich in der Regel voll und ganz auf den Kern des Problems. Das ist auch meistens richtig, aber eben nicht immer. Bei der Aufgabe: Wie bestrahlt man am besten einen Tumor, ohne zu viel gesundes Gewebe zu zerstören, ist die Lösung: Man bestrahlt es mit leichter Strahlung von allen Seiten. Die Strahlen bündeln sich im Tumor. Wird die Aufmerksamkeit der Versuchspersonen nicht auf den Tumor gelenkt, sondern auf das Gewebe drum herum (indem z.B. das Gewebe auf einer Abbildung auffällig rot dargestellt ist), fällt die Lösung der Aufgabe leichter. Man sollte also die Aufmerksamkeit auch mal vom Kernproblem lösen und auf Umliegendes oder auf Nebenaspekte richten.
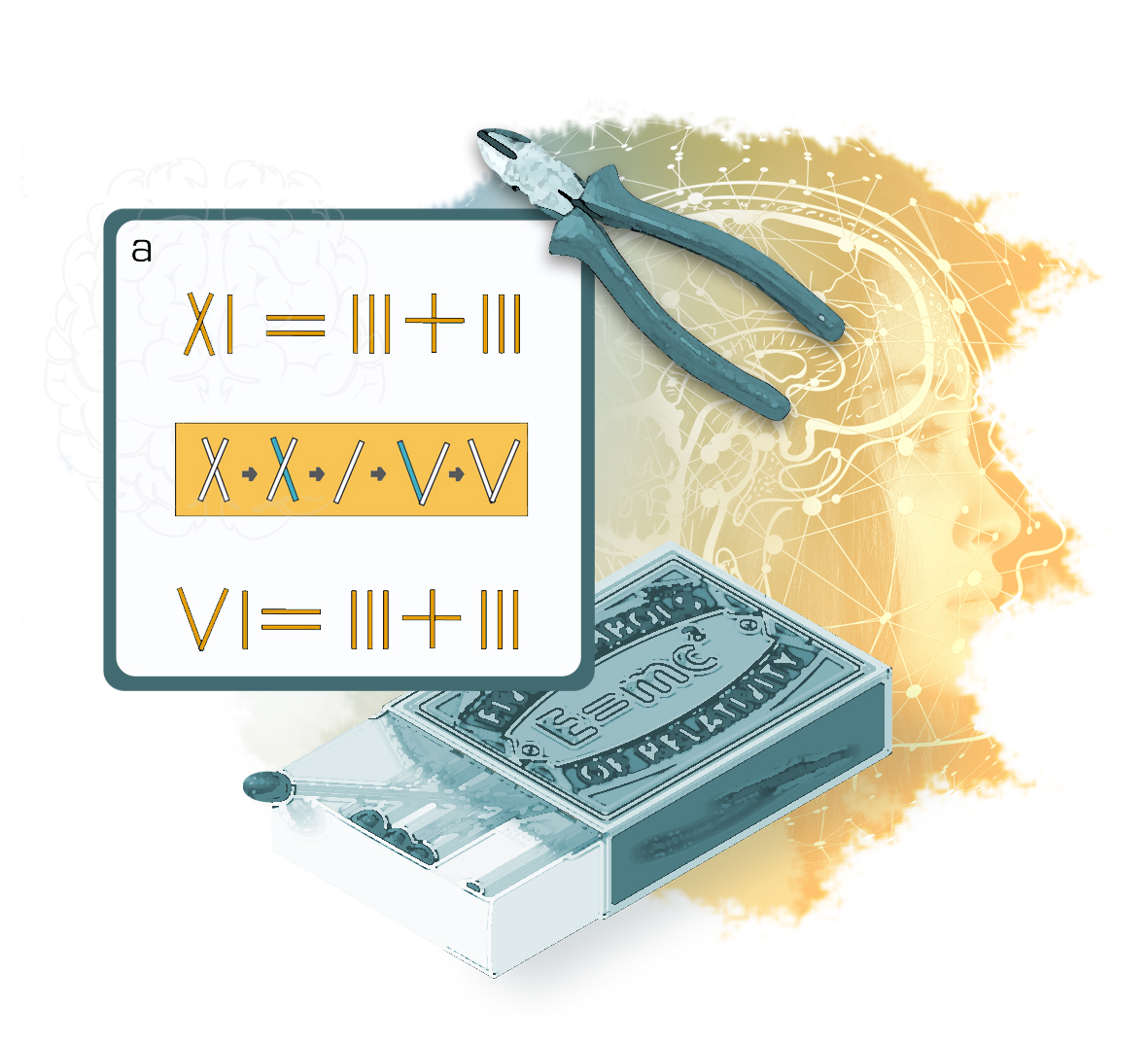
Selbst auferlegte Regeln und Grenzen
Das Beispiel für diese Denkfalle, siehe Abbildung b. Es handelt sich um 8 Münzen. Die Aufgabe lautet: Jede Münze soll drei andere Münzen berühren. Man darf dazu aber nur zwei Münzen bewegen. Wurde in der Aufgabenstellung verlangt, dass die Münzen dazu flach auf dem Tisch liegen bleiben müssen? Nein! Wir gehen aber trotzdem gerne automatisch davon aus, dass es ungültig ist, wenn man die Münzen aufeinander legt, was dann aber die Lösung ist. Man sollte also immer genau überlegen: Was ist die Aufgabe und was ist in der Aufgabenstellung wirklich verboten und welche Verbote bildet man sich nur ein?
Zwischenschritte / Umwege
Am liebsten haben wir es, wenn wir auf direktem Weg zur Lösung kommen. Wir sind dabei oft so sehr auf den direkten Weg fokussiert, dass der Blick für mögliche Umwege versperrt ist. Im Beispiel, Bild c, soll die Fläche (erstes Bild) berechnet werden, also die Fläche aus zwei komischen Dreiecken und einem komischen Parallelogramm. Man sieht nicht, dass es sich eigentlich um zwei leicht verschoben übereinanderliegende Dreiecke handelt. Verschiebt man diese, bevor man versucht über den direkten Weg die Aufgabe zu berechnen, hat man ein simples Rechteck, das sich ganz leicht berechnen lässt. Man sollte also immer überlegen, ob sich die Problem– Situation vielleicht anders organisieren / umstrukturieren lässt, um die Lösung einfacher zu machen.